Le coefficient de corrélation

Définition

La corrélation permet de savoir si les mesures de deux colonnes numériques sont liées, c'est à dire de répondre à la question : mes mesures varient-elles ensemble (liaison) ou sont-elles indépendantes l'une de l'autre (indépendance) ?

Le paramètre habituellement calculé est le coefficient de corrélation. Ce coefficient, noté r, est compris entre -1 et 1.

corrélation POSITIVE (r>0)

Plus la liaison est forte,

plus le coefficient est proche de 1.

Un coefficient de corrélation r=1 n'est en pratique jamais observé, hormis pour deux mesures identiques. Les points oranges seraient alors parfaitement alignés et dessineraient une droite.

corrélation nulle (r=0)

Moins la liaison est forte,

plus le coefficient est proche de 0.

Attention : le coefficient de corrélation ne recherche qu'une relation linéaire. Si la relation est d'une autre nature (exponentielle, en U, racine carré, etc.) le coefficient de corrélation sera faible ou nul alors même qu'une liaison existe.

corrélation Négative (r<0)

Plus la liaison est forte,

plus le coefficient est proche de -1.

Un coefficient de corrélation r=-1 n'est en pratique jamais observé, hormis pour deux mesures opposés. Les points oranges seraient alors parfaitement alignés et dessineraient une droite.

Rapport Student-Stats

Tableau

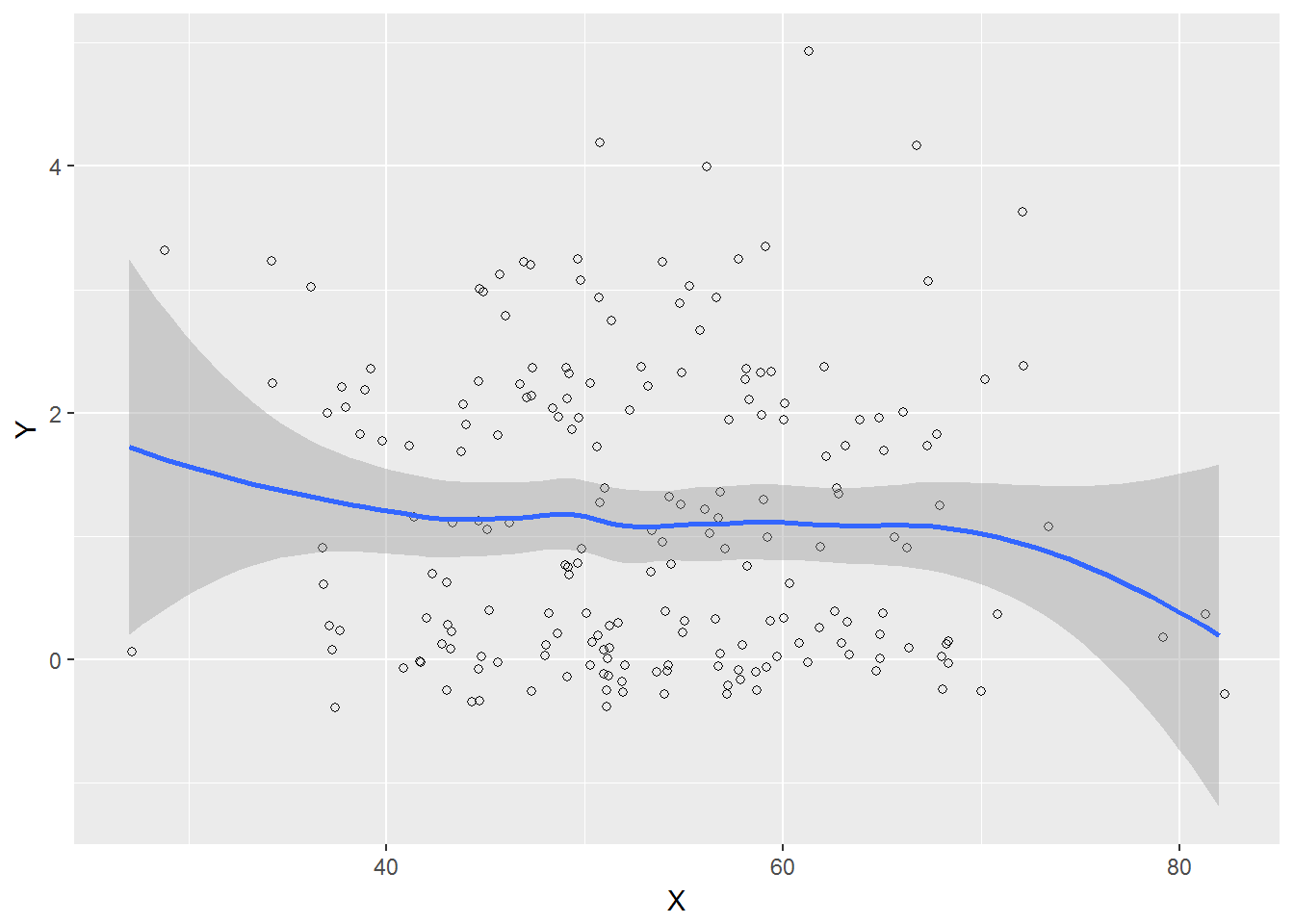
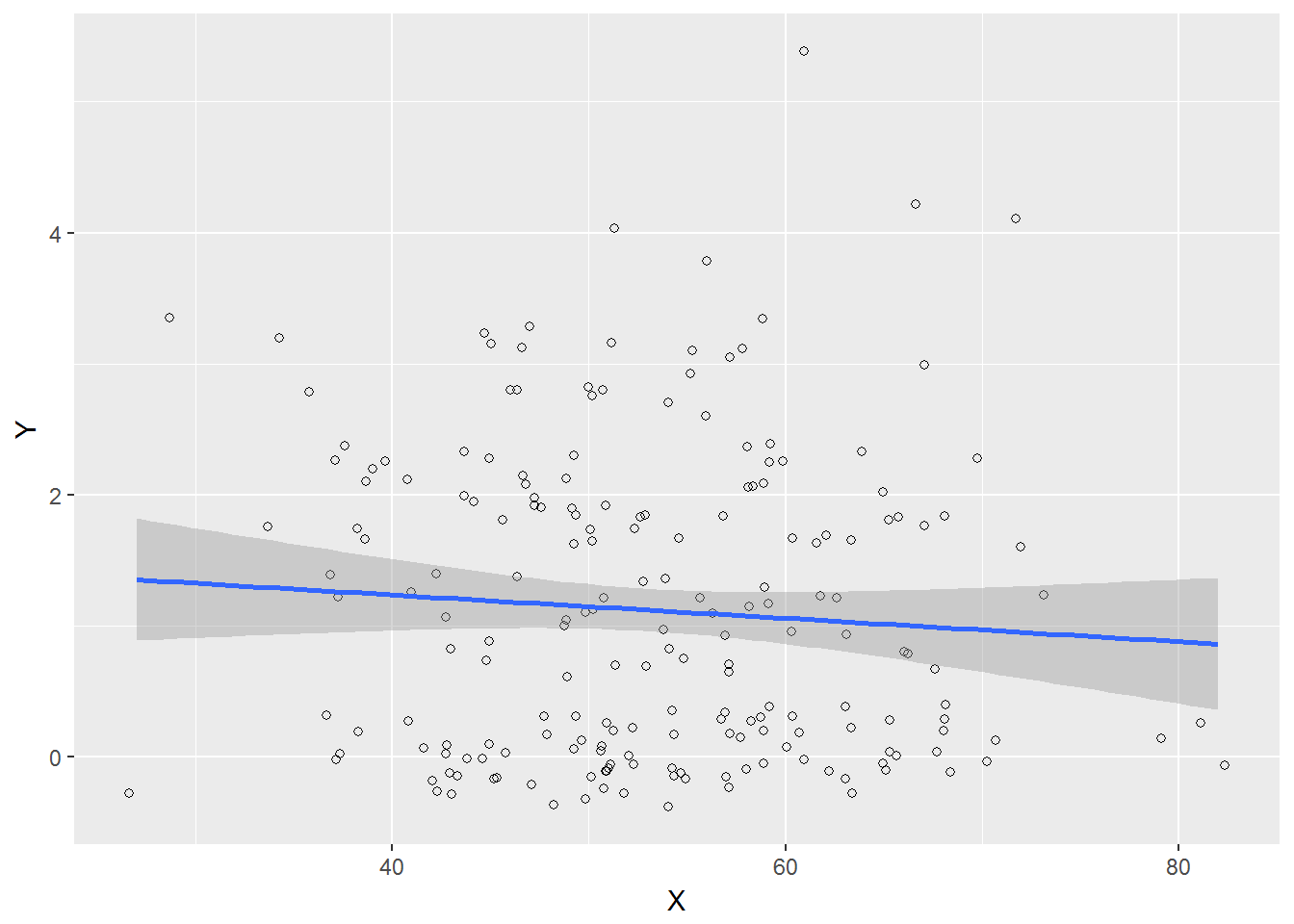
Représentation graphique

Si la relation est d'une autre nature que linéaire, alors le test n'est pas adapté et ne sera pas significatif. La première étape est d'observer l'allure de la relation sur ce graphique. Ici, on peut imaginer tracer une droite à l'intérieur de l'intervalle de confiance (zone grisée) : le test est adapté.

Moyennes mobiles

Si la relation est linéaire, alors on peut tracer la droite de régression correspondant au tableau récapitulatif. Les axes peuvent être inversés (Y~X ou X~Y) grâce aux boutons ci-dessus.

Droite de régression

Aide à la rédaction

Méthode

La corrélation entre deux variables quantitatives était mesurée grâce au coefficient de corrélation de Pearson. L’équivalent non-paramétrique (coefficient de Spearman) était préféré lorsque l’une des conditions d'application du test paramétrique n’étaient pas remplies. La significativité de la corrélation était déterminée grâce au test de nullité du coefficient de corrélation. Seuls les coefficients significativement différents de 0 étaient interprétés.

résultats

Si la corrélation est significative (p<0.05) :

Il existe une association linéaire [positive/négative] statistiquement significative entre [X] et [Y] : lorsque [X] [augmente/diminue], [Y] [augmente/diminue]. Le coefficient de corrélation [de Pearson/de Spearman] associé est égal à [valeur du coefficient de corrélation].

Si la corrélation n'est pas significative (p>=0.05) :

Il n’existe pas d'association linéaire statistiquement significative entre [X] et [Y].

Aide à l'interprétation

Test statistique

Le test de nullité du coefficient de corrélation permet de comparer la valeur du coefficient de corrélation à 0 :

Si le test est significatif, le coefficient de corrélation est significativement différent de 0 et on conclut à l'existence d' une liaison entre les deux mesures.
A l'inverse, si le test est non-significatif, on ne peut pas exclure l'absence de liaison.

Les autres paramètres

Coefficient de détermination : il est égal au carré du coefficient de corrélation et représente le pourcentage de variance partagé entre les deux mesures.

Équation de régression : on peut tracer la droite qui passe "le mieux" à travers le nuage de point. Lorsqu'on dispose d'une des deux valeurs, on peut facilement retrouvé l'autre valeur grâce à cette droite. On peut le faire graphiquement ou grâce aux deux équations en remplaçant l'une des deux valeurs. Attention : cette équation donne des résultats d'autant plus faux que le coefficient de corrélation se rapproche de 0. En effet, la relation n'est alors plus linéaire et la droite tracée est fausse. En pratique, n'utilisez cette équation que pour des liaisons fortes...

Pour aller plus loin...

Relation entre la puissance et le nombre de vitesse

Attention : le coefficient de corrélation ne recherche qu'une relation linéaire. Si la relation est d'une autre nature (exponentielle, en U, racine carré, etc.) le coefficient de corrélation sera faible ou nul alors même qu'une liaison existe.

La courbe de gauche (droite) est fausse car la relation recherchée est linéaire… La courbe de droite (en forme de “U”) est plus proche de la réalité, mais ne peut être mesurée avec un coefficient de corrélation. Lorsque la relation que vous observez n'est pas linéaire, il est préférable de ne pas faire apparaître le coefficient de corrélation dans vos résultats. Préférez plutôt un commentaire sur la forme de votre courbe.